Ya Gio (Giordano, no Giovanni) nos habló del valor P y su futilidad si no lo sabemos interpretar adecuadamente.
Ahora con la fiebre futbolera a nivel mundial, he hecho uso de un ejemplo similar al de Vickers y Michael Jordan, aunque lo ampliaré un poco más. Este ejemplo lo uso con frecuencia al dar clases de cómo interpretar la estadística para criticar un artículo.
Yo siempre he dicho que soy mejor que Cristiano Ronaldo (además de que tengo mejor físico que él) para anotar goles en tiros penales (penalties). El señor Ronaldo, indignado, me reta a una competencia de tiros penales (y una apuesta económica) para demostrarme que él es mejor. Yo acepto el reto, pero con la condición de que yo, como científico, haré uso de las matemáticas y de mi nuevo software para calcular un valor P y ver si la diferencia que exista en los goles anotados es significativa o no; es decir, si es por azar.
Mi otra condición es que tenemos que fijar ANTES de empezar a tirar los penalties, el número de intentos que cada quien hará.
Ronaldo me mira fijamente con vacilación y finalmente “calcula” y dice un número:
– De acuerdo, tiremos diez veces cada quien –me dice – con eso te demuestro que soy mejor
– Ok –respondo, y mi mente ríe, pero yo me mantengo frío para que no se dé cuenta de mi plan.
Comienza él con sus diez tiros. El portero será el mismo para los dos para que no exista sesgo. Mete 8 goles de los 10 tiros. Entonces sigo yo… y meto 4 de los 10 tiros…
– ¡Já¡ –dice Cristiano- ¡gané!
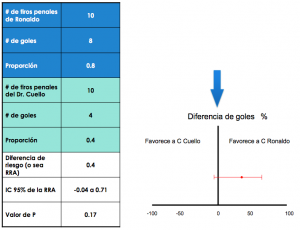
– No tan rápido –extraigo mi laptop y empiezo a calcular, mostrándole la siguiente tabla:
Si estuviésemos contando solamente quién mete más goles, él hubiera ganado; pero no fue así; nuestro trato era comprobar que él es mejor que yo estadísticamente. Así que usando un software estadístico obtengo que el valor P = 0.17
– Según esto –le digo al futbolista- NO eres mejor que yo, fue suerte. Es decir, la diferencia que acabas de ver entre tú y yo es probable que se deba simplemente al azar, y según las reglas de los estadísticos, esa probabilidad tiene que ser menor al 5% para decir que tú ó yo somos diferentes. Hasta dado ese caso, entonces podría aceptar que tú eres mejor que yo.
– ¡Pero si yo metí el doble de goles! –replica- ¿cómo es posible?
– Las matemáticas no fallan. La probabilidad de que esta diferencia que vimos sea debida al azar es del 17% y recuerda, tiene que ser menor al 5% (p menor a 0,05)
– ¡No! –insiste- tiremos más para demostrarte que soy mejor.
– Lo haría, pero a priori fijamos el número de tiros, y de hecho tú lo calculaste… no sé cómo, pero lo calculaste.
Este ejercicio mental entre Ronaldo y Cuello (así es, fue una simulación) nos sirve para dos cosas principalmente:
1. INTERPRETAR EL VALOR P Y CONOCER LOS INTERVALOS DE CONFIANZA
En la figura se puede ver una flecha azul. Esta indica una diferencia de cero entre Ronaldo y yo, es decir, mi hipótesis nula. También se puede ver que Ronaldo metió el 80% de sus tiros, y yo metí el 40%; la diferencia entre ambos fue de 40% (ó 0,4) a favor de Cristiano.
El valor p=0,17 nos dice: la probabilidad de que esa diferencia (o una mayor) sea debida al azar es, en este caso, del 17% .
El error de Cristiano fue no pedir intervalos de confianza del 95% (IC95%). Afortunadamente no vio la gráfica, ya que pudo argumentar mejor con la misma. Y es cierto, al verla podemos apreciar la diferencia entre él y yo, pero con el IC95% de esa diferencia.
El IC95% nos dice el grado de certidumbre, o dicho de otra forma, de DÓNDE ESTÁ LA VERDAD. En otros términos, si repitiera nuestro experimento miles de veces, puedo decir, con un 95% de certeza, que el resultado, o la verdad, “caerá” entre estos dos puntos que se ven en la gráfica, y que va desde -0,04 (a favor mío) hasta 0,71 (a favor de Ronaldo).
Viendo esto, Ronaldo podría haber dicho que hay una tendencia a su favor, y aunque matemáticamente no se demostró significancia, puede ser debido a muchos otros factores, como en este caso, por ejemplo, simplemente con aumentar el tamaño de la muestra.
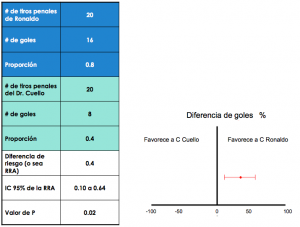
¿Qué pasa si aumentamos el número de tiros penales a 20 cada quien? obtendríamos la siguiente gráfica.
La diferencia sigue siendo del 40%, y aquí ya observamos que el IC95% está por completo a favor de Cristiano. Es decir, la certeza o la verdad se hace más estrecha, y que la diferencia será de cuando menos un 0,10 (10%) y cuando mucho del 0,65 (65%), pero ambas cifras a favor de Cristiano. A más tiros penales, mayor el grado de certeza.
¿Y nuestro amigo el valor P? En este caso resulta en 0,02; ahora sí es “significativo”, es decir, menor a 0,05
Posterior a esto no tiene caso seguir tirando penales. Sería insubstancial y grosero a mi persona; ya Cristiano demostró que es mejor que yo, con tan solo 20 tiros cada quien.
2. CONOCER LA IMPORTANCIA DEL TAMAÑO DE MUESTRA
El error de Cristiano fue no definir a priori el tamaño de la muestra de forma correcta. Y no saber que el tamaño de muestra depende de la diferencia que se espera encontrar entre dos intervenciones. Es decir, para calcular el número de tiros penales, debió haber pensado cuánto en promedio mete él en goles, y cuánto en promedio podría meter yo, y preguntarse ¿qué diferencia se consideraría como “clínicamente” significativa?
Si hubiese sacado un programa de estadística y colocar como proporción 1 (él) de 0.8 y proporción 2 (yo) de 0.4; hubiese visto que con 20 tiros penales era suficiente para rechazar la hipótesis nula (con un 95% de certeza).
Si Ronaldo me hubiese pedido el intervalo de confianza 95% (IC95%) tal vez tendría más argumentos para que yo repitiera el ejercicio con más tiros.
Pero yo decidí entonces traer a alguien de su “tamaño”: a Lionel Messi.
Con este jugador, la pregunta que tenemos que hacer es “¿Cuántos tiros penales serán necesarios que tire cada uno para demostrar que uno es mejor que el otro?” “¿qué diferencia esperamos encontrar?” Usando el mismo software, yo asumo que Ronaldo meterá el 80% de los goles, mientras que Messi meterá el 83% de los goles (o al revés). No importa, esa diferencia la consideraré como significativa. Siendo así, requieren tirar… ¡2629 tiros cada quien!
En los trabajos de investigación ocurre algo similar. El investigador debe definir a priori su tamaño de muestra, dependiendo de la diferencia que consideraría significativa, determinada por él mismo. Esto es una necesidad desde el punto de vista ético y económico, para evitar gastos innecesarios y evitar que los investigadores sigan reclutando pacientes en una cantidad indeterminada.
Recordemos que el valor P y su significancia estadística (menor a 0,05) se fijó arbitrariamente por los científicos, y como comentó Giordano en el post previo, sólo nos dice una probabilidad. Es bueno que sepamos qué es, pero exijamos mejor el IC95% para darnos una mejor idea de los resultados.
Centro de Medicina Basada en Evidencia del Tecnológico de Monterrey