El RR, o riesgo relativo o razón de riesgos, aparece frecuentemente en artículos de tratamiento y sobre todo en revisiones sistemáticas. Y ahí también nos topamos a su «primo», el OR (odds ratio o razón de momios). Por lo general, una manera de ilustrar estos valores o resultados es mediante el uso de una «T» invertida, así:
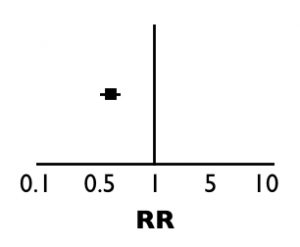 Pero, ¿qué significa que un RR esté por debajo de 1? ¿o en la gráfica, a la izquierda del 1?
Pero, ¿qué significa que un RR esté por debajo de 1? ¿o en la gráfica, a la izquierda del 1?
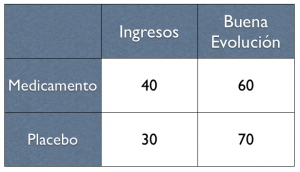
Supongamos que tenemos una población enferma y queremos saber si un medicamento funciona para reducir los ingresos hospitalarios. Para comprobarlo, hacemos un experimento (un ensayo clínico aleatorio) donde a un grupo de pacientes le damos el medicamento, al otro grupo le damos un placebo, y al cabo de cierto tiempo vemos cuántos se hospitalizaron de cada grupo.
Imaginemos que estos fueron los resultados:
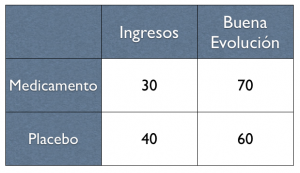 Es muy visible que hubo menos ingresos en el grupo de pacientes que recibieron el medicamento. Si yo hubiera sido uno de los pacientes que recibieron el medicamento, ¿cuál es mi riesgo de hospitalización? Fácil, se hospitalizaron 30 de 100 pacientes en el grupo del tratamiento, por lo tanto, es un riesgo del 30%. (por lo visto, nuestra enfermedad hipotética es bastante agresiva, pero bueno, continuemos)
Es muy visible que hubo menos ingresos en el grupo de pacientes que recibieron el medicamento. Si yo hubiera sido uno de los pacientes que recibieron el medicamento, ¿cuál es mi riesgo de hospitalización? Fácil, se hospitalizaron 30 de 100 pacientes en el grupo del tratamiento, por lo tanto, es un riesgo del 30%. (por lo visto, nuestra enfermedad hipotética es bastante agresiva, pero bueno, continuemos)
¿Y si yo hubiera sido uno de los pacientes que recibieron el placebo? Mi riesgo de hospitalización sería del 40% (40 de 100 se hospitalizaron).
El famoso RR es simplemente la división entre los riesgos de ambos grupos. En nuestro ejemplo: 0.3/0.4 = 0.75. El RR fue menor de 1. Si reflexionamos un poco en el resultado, el RR fue menor de 1 porque hubo menos eventos (hospitalizaciones) en el grupo tratado. En la «T» invertida, el punto que representa al 0.75 estaría a la izquierda del 1:
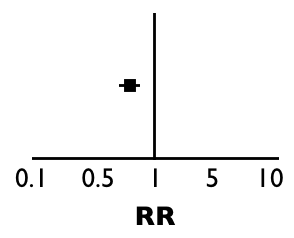 En cambio, si los resultados hubieran sido así:
En cambio, si los resultados hubieran sido así:
Ahora el RR sería mayor de 1, ¿cierto? Es decir, hubo más eventos (más hospitalizados) en el grupo tratado (0.4/0.3 = 1.33). En este caso, el punto del resultado estaría a la derecha de la «T» invertida:
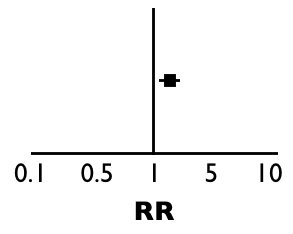 Entonces, cuando el punto (la estimación del efecto de un medicamento o una exposición) está a la izquierda, significa que el grupo tratado/expuesto tuvo menos eventos que el grupo control. Cuando el punto está a la derecha, significa que el grupo tratado/expuesto tuvo más eventos que el grupo control.
Entonces, cuando el punto (la estimación del efecto de un medicamento o una exposición) está a la izquierda, significa que el grupo tratado/expuesto tuvo menos eventos que el grupo control. Cuando el punto está a la derecha, significa que el grupo tratado/expuesto tuvo más eventos que el grupo control.
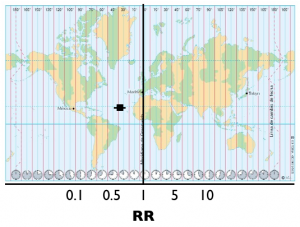
Un colega hizo la analogía con los husos horarios. Viendo el mapa, los lugares a la izquierda del meridiano de Greenwich van teniendo menos horas. Los lugares a la derecha van teniendo más horas.
 Cabe mencionar que si un RR es menor a 1 (a la izquierda) no quiere decir que el medicamento sea bueno. Si los eventos que estamos evaluando son malos (ej. defunciones, hospitalizaciones, infecciones), entonces sí queremos que haya menos en los tratados. Pero si lo que estamos tratando de medir son eventos buenos (ej. resolución del dolor), entonces queremos que el RR sea mayor a 1, o a la derecha en la «T» invertida.
Cabe mencionar que si un RR es menor a 1 (a la izquierda) no quiere decir que el medicamento sea bueno. Si los eventos que estamos evaluando son malos (ej. defunciones, hospitalizaciones, infecciones), entonces sí queremos que haya menos en los tratados. Pero si lo que estamos tratando de medir son eventos buenos (ej. resolución del dolor), entonces queremos que el RR sea mayor a 1, o a la derecha en la «T» invertida.
Un RR de 0.5 significa que hubo la mitad de eventos en los pacientes tratados en comparación con el grupo control. Y un RR de 2 significa que hubo el doble de eventos en los tratados en comparación con el grupo control. Pero siempre debemos recordar que el RR es relativo, y que puede ser más impresionante que los términos absolutos.
Giordano Pérez Gaxiola
Departamento de Medicina Basada en la Evidencia
Hospital Pediátrico de Sinaloa